Ratio of area of two nested polygons formed by connecting midpoints of sides of a regular N-sided polygon

Ratio of area of two nested polygons formed by connecting midpoints of sides of a regular N-sided polygon

Given an N-sided polygon, the task is to find the ratio of the area of the N^th to (N + 1)^th N-sided regular nested polygons generated by joining the midpoints of the sides of the original polygon.

Examples :

Input: N = 3
Output: 4.000000
Explanation:

Nested Triangle

Ratio of the length of the sides formed by joining the mid-points of the triangle with the length of the side of the original triangle is 0.5. Hence, R = (Area of N^th triangle) / (Area of (N + 1)^th triangle) = 4

Input: N = 4
Output: 2.000000

Approach: The problem can be solved based on the following observations:

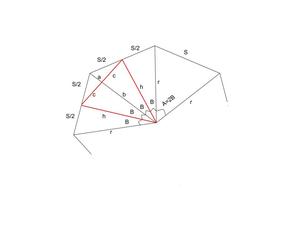
• Consider an N-sided regular polygon as shown in the figure below.
  

  
  Representation Of Nested regular polygon of N sides.

• A = 2 * ℼ / N
  B = ℼ / N
  h = r * cos(B)
  b = h * cos(B)
  c = h((1 – cos(A)) / 2)^1/2
• Area of the Black Isosceles Triangle:

• Area of the Red Isosceles Triangle:

• r = s / (2 * [1 – cos(2B)])^1/2 and b = r * [cos(B)]²
• After combining the above equations:

• Final result obtained is as follows:

Below is the implementation of the above approach:

C++

#include <bits/stdc++.h> using namespace std;    void AreaFactor(int n) {          double pi = 3.14159265;             double areaf = 1 / (cos(pi / n)                         * cos(pi / n));                  cout << fixed << setprecision(6)          << areaf << endl; }    int main() {     int n = 4;     AreaFactor(n);        return 0; }

Output:

2.000000

Time Complexity: O(1)
Auxiliary Space: O(1)

Attention reader! Don’t stop learning now. Get hold of all the important mathematical concepts for competitive programming with the Essential Maths for CP Course at a student-friendly price. To complete your preparation from learning a language to DS Algo and many more,  please refer Complete Interview Preparation Course.

Adblock test (Why?)

Original page link

Best Cool Tech Gadgets

Top favorite technology gadgets