Size of smallest square that contains N non-overlapping rectangles of given dimensions

Size of smallest square that contains N non-overlapping rectangles of given dimensions

Given two positive integers W and H and N rectangles of dimension W*H, the task is to find the smallest size of the square required such that all the N rectangles can be packed without overlapping. 

Examples:

Input: N = 10, W = 2, H = 3
Output: 9
Explanation:
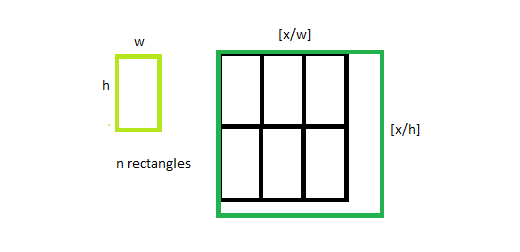
The smallest size of the square is 9 units to pack the given 10 rectangles of size 2*3 as illustrated in the below image:

Input: N = 1, W = 3, H = 3
Output: 3

Approach: The given problem is based on the following observations:

• It can be shown that one of the optimal spacing of rectangles within a square is given by:

• The maximum number of rectangles of dimension W*H, that can be fitted in the square with sides X is given by ⌊X/W⌋⋅⌊X/H⌋.
• The above function is monotonically increasing. Therefore, the idea is to use the Binary Search to find the smallest side of a square that satisfies the given condition.

Follow the steps below to solve the problem:

• Initialize two variables, say low as 1, and high as W*H*N.
• Iterate until i is less than j and perform the following steps:
  • Find the value of mid as (i + j)/2.
  • Now, if the value (mid/W)*(mid/H) is at most N, then update the value of high as mid.
  • Otherwise, update the value of low as (mid + 1).
• After completing the above steps, print the value of high as the resultant value.

Below is the implementation of the above approach:

Python3

def bound(w, h, N, x):                  val = (x//w)*(x//h)                      if(val >= N):         return True                   else:         return False    def FindSquare(N, W, H):             i = 1                 j = W * H*N                 while(i < j):                           mid = i + (j - i)//2                              if(bound(W, H, N, mid)):             j = mid                             else:             i = mid + 1                  return j       W = 2 H = 3 N = 10    print(FindSquare(N, W, H))

Time Complexity: O(log(W*H))
Auxiliary Space: O(1)

Attention reader! Don’t stop learning now. Get hold of all the important DSA concepts with the DSA Self Paced Course at a student-friendly price and become industry ready.

Let's block ads! (Why?)

Original page link

Best Cool Tech Gadgets

Top favorite technology gadgets